迷你浮點數

迷你浮點（minifloats）是用少位元浮點數值。不太適合通用數值計算。通常用於特殊目的，像電腦圖形學，迭代很小並且精度具有美學效果。^[1]機器學習也使用類似格式，如bfloat16。

Minifloats按照IEEE 754標準設計。必須遵守次正規數和正規數之間邊界規則（未明確寫入的），且具無限大和 NaN 特殊模式。標準化數字以有偏差的指數儲存。該標準的新修訂版 IEEE 754-2008 具有 16 位元二進位小型浮點數。

符號[编辑]

迷你浮點通常使用四個數字的元組（S、E、M、B）來描述：

S是符號欄位的長度。通常為 0 或 1。
E是指數欄位的長度。
M是尾數（有效數字）欄位的長度。
B是指數偏差。

因此，以 (S, E, M, B) 表示的小型浮點格式為 S + E + M 位元。 (S, E, M, B) 表示法可以轉換為 (B, P, L, U) 格式，如 (2, M + 1, B + 1, 2 S − B) (IEEE指數）。

例子[编辑]

8位元 minifloat 範例(1.4.3)
符號	指數				有效數
0	0	0	0	0	0	0	0

具有1個符號位元、4個指數位元和3個有效位元^[2]^[3]對於大多數值指數x是 $2 x -7$ 。所有IEEE 754原則都應該有效。 ^[4]

零的表示[编辑]

0 0000 000 = 0
1 0000 000 = −0

次正規數[编辑]

有效數用0.擴展：

0 0000 001 = 0.001₂ × 2^{1 - 7} = 0.125 × 2^-6 = 0.001953125 (最小次正規數)
...
0 0000 111 = 0.111₂ × 2^{1 - 7} = 0.875 × 2^-6 = 0.013671875 (最大次正規數)

標準化數字[编辑]

有效數用1.擴展：

0 0001 000 = 1.000₂ × 2^{1 - 7} = 1 × 2^-6 = 0.015625 (least normalized number)
0 0001 001 = 1.001₂ × 2^{1 - 7} = 1.125 × 2^-6 = 0.017578125
...
0 0111 000 = 1.000₂ × 2^{7 - 7} = 1 × 2⁰ = 1
0 0111 001 = 1.001₂ × 2^{7 - 7} = 1.125 × 2⁰ = 1.125 (最小值大於 1)
...
0 1110 000 = 1.000₂ × 2^{14 - 7} =  1.000 × 2⁷ =  128
0 1110 001 = 1.001₂ × 2^{14 - 7} =  1.125 × 2⁷ =  144
...
0 1110 110 = 1.110₂ × 2^{14 - 7} =  1.750 × 2⁷ = 224
0 1110 111 = 1.111₂ × 2^{14 - 7} =  1.875 × 2⁷ = 240 (最大標準數)

無窮[编辑]

0 1111 000 = +∞
1 1111 000 = −∞

非數[编辑]

s 1111 mmm = NaN (if mmm ≠ 000)

數值表[编辑]

這是此範例 8 位元浮點的所有可能值的圖表。

	… 000	… 001	… 010	… 011	… 100	… 101	… 110	… 111
0 0000 …	0	0.001953125	0.00390625	0.005859375	0.0078125	0.009765625	0.01171875	0.013671875
0 0001 …	0.015625	0.017578125	0.01953125	0.021484375	0.0234375	0.025390625	0.02734375	0.029296875
0 0010 …	0.03125	0.03515625	0.0390625	0.04296875	0.046875	0.05078125	0.0546875	0.05859375
0 0011 …	0.0625	0.0703125	0.078125	0.0859375	0.09375	0.1015625	0.109375	0.1171875
0 0100 …	0.125	0.140625	0.15625	0.171875	0.1875	0.203125	0.21875	0.234375
0 0101 …	0.25	0.28125	0.3125	0.34375	0.375	0.40625	0.4375	0.46875
0 0110 …	0.5	0.5625	0.625	0.6875	0.75	0.8125	0.875	0.9375
0 0111 …	1	1.125	1.25	1.375	1.5	1.625	1.75	1.875
0 1000 …	2	2.25	2.5	2.75	3	3.25	3.5	3.75
0 1001 …	4	4.5	5	5.5	6	6.5	7	7.5
0 1010 …	8	9	10	11	12	13	14	15
0 1011 …	16	18	20	22	24	26	28	30
0 1100 …	32	36	40	44	48	52	56	60
0 1101 …	64	72	80	88	96	104	112	120
0 1110 …	128	144	160	176	192	208	224	240
0 1111 …	∞	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1 0000 …	−0	−0.001953125	−0.00390625	−0.005859375	−0.0078125	−0.009765625	−0.01171875	−0.013671875
1 0001 …	−0.015625	−0.017578125	−0.01953125	−0.021484375	−0.0234375	−0.025390625	−0.02734375	−0.029296875
1 0010 …	−0.03125	−0.03515625	−0.0390625	−0.04296875	−0.046875	−0.05078125	−0.0546875	−0.05859375
1 0011 …	−0.0625	−0.0703125	−0.078125	−0.0859375	−0.09375	−0.1015625	−0.109375	−0.1171875
1 0100 …	−0.125	−0.140625	−0.15625	−0.171875	−0.1875	−0.203125	−0.21875	−0.234375
1 0101 …	−0.25	−0.28125	−0.3125	−0.34375	−0.375	−0.40625	−0.4375	−0.46875
1 0110 …	−0.5	−0.5625	−0.625	−0.6875	−0.75	−0.8125	−0.875	−0.9375
1 0111 …	−1	−1.125	−1.25	−1.375	−1.5	−1.625	−1.75	−1.875
1 1000 …	−2	−2.25	−2.5	−2.75	−3	−3.25	−3.5	−3.75
1 1001 …	−4	−4.5	−5	−5.5	−6	−6.5	−7	−7.5
1 1010 …	−8	−9	−10	−11	−12	−13	−14	−15
1 1011 …	−16	−18	−20	−22	−24	−26	−28	−30
1 1100 …	−32	−36	−40	−44	−48	−52	−56	−60
1 1101 …	−64	−72	−80	−88	−96	−104	−112	−120
1 1110 …	−128	−144	−160	−176	−192	−208	−224	−240
1 1111 …	−∞	NaN	NaN	NaN	NaN	NaN	NaN	NaN

只有 242 個不同的非 NaN 值（如果 +0 和 -0 視為不同），因為 14 個位元模式代表 NaN。

可以使用腳本為 SEMB 值的任意組合產生如上所述的表格Python 或GDScript.

其它偏差值[编辑]

在這些小尺寸下，其它偏差值可能會很有趣，例如 -2 的偏差將使數字 0-16 具有與整數 0-16 相同的位表示形式，但會導致無法表示非整數值。

0 0000 000 = 0.000₂ × 2^{1 - (-2)} = 0.0 × 2³ = 0 (subnormal number)
0 0000 001 = 0.001₂ × 2^{1 - (-2)} = 0.125 × 2³ = 1 (subnormal number)
0 0000 111 = 0.111₂ × 2^{1 - (-2)} = 0.875 × 2³ = 7 (subnormal number)
0 0001 000 = 1.000₂ × 2^{1 - (-2)} = 1.000 × 2³ = 8 (normalized number)
0 0001 111 = 1.111₂ × 2^{1 - (-2)} = 1.875 × 2³ = 15 (normalized number)
0 0010 000 = 1.000₂ × 2^{2 - (-2)} = 1.000 × 2⁴ = 16 (normalized number)

Arithmetic[编辑]

Addition[编辑]

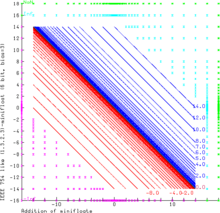
此圖示範了增加較小的 (1.3.2.3)-6 位元迷你浮點。

此浮點系統完全遵循IEEE 754規則。

NaN作為運算元始終產生NaN結果。

∞−∞和 (−∞) +∞會產生 NaN（綠）。∞可以按有限值增減而不會發生變化。

有限操作數的和可以給出無限結果（即 14.0 + 3.0 = +∞，因為結果是青，-∞紅）。

算術運算可以類似地說明：

減法
乘法
除法

已隱藏部分未翻譯内容，歡迎參與翻譯。

Other sizes[编辑]

The Radeon R300 and R420 GPUs used an "fp24" floating-point format with 7 bits of exponent and 16 bits (+1 implicit) of mantissa.^[5] "Full Precision" in Direct3D 9.0 is a proprietary 24-bit floating-point format. Microsoft's D3D9 (Shader Model 2.0) graphics API initially supported both FP24 (as in ATI's R300 chip) and FP32 (as in Nvidia's NV30 chip) as "Full Precision", as well as FP16 as "Partial Precision" for vertex and pixel shader calculations performed by the graphics hardware.

Khronos defines 10-bit and 11-bit float formats for use with Vulkan. Both formats have no sign bit and a 5-bit exponent. The 10-bit format has a 5-bit mantissa, and the 11-bit format has a 6-bit mantissa.^[6]^[7]

4 bits and fewer[编辑]

The smallest possible float size that follows all IEEE principles, including normalized numbers, subnormal numbers, signed zero, signed infinity, and multiple NaN values, is a 4-bit float with 1-bit sign, 2-bit exponent, and 1-bit mantissa.^[8] In the table below, the columns have different values for the sign and mantissa bits, and the rows are different values for the exponent bits.

	0 … 0	0 … 1	1 … 0	1 … 1
… 00 …	0	0.5	−0	−0.5
… 01 …	1	1.5	−1	−1.5
… 10 …	2	3	−2	−3
… 11 …	∞	NaN	−∞	NaN

If normalized numbers are not required, the size can be reduced to 3-bit by reducing the exponent down to 1.

	0 … 0	0 … 1	1 … 0	1 … 1
… 0 …	0	1	−0	−1
… 1 …	∞	NaN	−∞	NaN

In situations where the sign bit can be excluded, each of the above examples can be reduced by 1 bit further, keeping only the left half of the above tables. A 2-bit float with 1-bit exponent and 1-bit mantissa would only have 0, 1, Inf, NaN values.

If the mantissa is allowed to be 0-bit, a 1-bit float format would have a 1-bit exponent, and the only two values would be 0 and Inf. The exponent must be at least 1 bit or else it no longer makes sense as a float (it would just be a signed number).

In embedded devices[编辑]

Minifloats are also commonly used in embedded devices,^{[來源請求]} especially on microcontrollers where floating-point will need to be emulated in software. To speed up the computation, the mantissa typically occupies exactly half of the bits, so the register boundary automatically addresses the parts without shifting.

參見[编辑]

參考[编辑]

^ Mocerino, Luca; Calimera, Andrea. AxP: A HW-SW Co-Design Pipeline for Energy-Efficient Approximated ConvNets via Associative Matching. Applied Sciences. 24 November 2021, 11 (23): 11164. doi:10.3390/app112311164 .
^ IEEE half-precision has 5 exponent bits with bias 15 ( $2^{5-1}-1=15$ ), IEEE single-precision has 8 exponent bits with bias 127 ( $2^{8-1}-1=127$ ), IEEE double-precision has 11 exponent bits with bias 1023 ( $2^{11-1}-1=1023$ ), and IEEE quadruple-precision has 15 exponent bits with bias 16383 ( $2^{15-1}-1=16383$ ). See the Exponent bias article for more detail.
^ O'Hallaron, David R.; Bryant, Randal E. Computer systems: a programmer's perspective 2. Boston, Massachusetts, USA: Prentice Hall. 2010. ISBN 978-0-13-610804-7.
^ Burch, Carl. Floating-point representation. Hendrix College. [2023-08-29].
^ Buck, Ian, Chapter 32. Taking the Plunge into GPU Computing, Pharr, Matt (编), GPU Gems, 2005-03-13 [2018-04-05], ISBN 0-321-33559-7 .
^ Garrard, Andrew. 10.3. Unsigned 10-bit floating-point numbers. Khronos Data Format Specification v1.2 rev 1. Khronos Group. [2023-08-10].
^ Garrard, Andrew. 10.2. Unsigned 11-bit floating-point numbers. Khronos Data Format Specification v1.2 rev 1. Khronos Group. [2023-08-10].
^ Shaneyfelt, Dr. Ted. Dr. Shaneyfelt's Floating Point Consruction Gizmo. Dr. Ted Shaneyfelt. [2023-08-29].

Munafo, Robert. Survey of Floating-Point Formats. 15 May 2016 [8 August 2016].

外部連結[编辑]

OpenGL half float pixel

[1] Mocerino, Luca; Calimera, Andrea. AxP: A HW-SW Co-Design Pipeline for Energy-Efficient Approximated ConvNets via Associative Matching. Applied Sciences. 24 November 2021, 11 (23): 11164. doi:10.3390/app112311164 .

[2] IEEE half-precision has 5 exponent bits with bias 15 ( $2^{5-1}-1=15$ ), IEEE single-precision has 8 exponent bits with bias 127 ( $2^{8-1}-1=127$ ), IEEE double-precision has 11 exponent bits with bias 1023 ( $2^{11-1}-1=1023$ ), and IEEE quadruple-precision has 15 exponent bits with bias 16383 ( $2^{15-1}-1=16383$ ). See the Exponent bias article for more detail.

[Bryant_2010-3] O'Hallaron, David R.; Bryant, Randal E. Computer systems: a programmer's perspective 2. Boston, Massachusetts, USA: Prentice Hall. 2010. ISBN 978-0-13-610804-7.

[4] Burch, Carl. Floating-point representation. Hendrix College. [2023-08-29].

[5] Buck, Ian, Chapter 32. Taking the Plunge into GPU Computing, Pharr, Matt (编), GPU Gems, 2005-03-13 [2018-04-05], ISBN 0-321-33559-7 .

[6] Garrard, Andrew. 10.3. Unsigned 10-bit floating-point numbers. Khronos Data Format Specification v1.2 rev 1. Khronos Group. [2023-08-10].

[7] Garrard, Andrew. 10.2. Unsigned 11-bit floating-point numbers. Khronos Data Format Specification v1.2 rev 1. Khronos Group. [2023-08-10].

[8] Shaneyfelt, Dr. Ted. Dr. Shaneyfelt's Floating Point Consruction Gizmo. Dr. Ted Shaneyfelt. [2023-08-29].

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

微處理器
字
1 2（英语：2-bit） 4 8 12 16 18（英语：18-bit） 24（英语：24-bit） 26（英语：26-bit） 31（英语：31-bit） 32 36（英语：36-bit） 48（英语：48-bit） 60（英语：60-bit） 64 128 256 512（英语：512-bit）
應用
8 16 32 64
二進制浮點精度
16 32 40（英语：Extended precision） 64 80（英语：Extended precision） 128（英语：Quadruple-precision floating-point format） 256（英语：Octuple-precision floating-point format） ×½ ×1 ×2 ×4（英语：Quadruple-precision floating-point format） ×8（英语：Octuple-precision floating-point format）
資料大小
Nibble（英语：nibble） octet / byte word dword qword DQWord
查论编